2進数の基本
0と1という2つの数字を使って数をあらわしたものが2進数です。1から順に2進数で数をあらわすと下のようになります。
\(1\) \(10\) \(11\) \(100\) \(101\) \(110\) \(111\) \(1000\) \(1001\)・・・
2進数と他の進数の変換
2進数から10進数へ
10進数とは、0から9までの数で数字をあらわしたものです。2進数を10進数に変換するために「2進数の各桁の大きさを10進数であらわすとどうなるか」について考えましょう。2進数の001は10進数で1、2進数の010は10進数で2、2進数の100は10進数の4…桁が大きくなるごとに、10進数では2の乗数と同じように大きくなっていきます。各桁の大きさを足し合わせることによって2進数を10進数に変換することができます。
\(1\times2^0+1\times2^1+1\times2^2+1\times2^3\)・・・
0から8までの数で数字をあらわした8進数や、0からFであらわした16進数も同様に、各桁の大きさを10進数で考えて、足し合わせることによって10進数に変換することが出来ます。
8進数や16進数
8進数の桁の大きさを10進数であらわすと2の3乗になります。これは2進数の3桁分の大きさと同じです。そのため2進数を3桁ずつ10進数に直すことによって、2進数を8進数に変換することが出来ます。16進数も同様ですが、9以上の数字になった場合は16進数の表記に従って、10はA、11はB、12はC・・・のように変換してください。
例1:2進数の11111100を8進数に変換する場合
\(11/111/100\) → \(384\)
例2:2進数の11111100を16進数に変換する場合
\(1111/1100\) → \(FC\)
10進数から2進数へ
先ほどの2進数を10進数に変換する方法を用いて考えます。10進数をN、2進数の1桁目をB0、2桁目をB1…n桁目までとすると
\(N=B_0\times2^0+B_1\times2^1+B_2\times2^2+B_3\times2^3\)・・・\(B_n\times2^n\)
2のB1以降の式を2で括ると次のようになります。2の0乗は1なので2で括ることはできません。
\(N=B_0+2(B_1+B_2\times2^1+B_3\times2^2+B_4\times2^3\)・・・\(B_n\times2^{n-1})\)
この式から、B0はNを2で割った時のあまりに相当することが分かります。また、2で括られた式が2進数の2桁以降になっています。そのため、n桁目になるまでこれを繰り返せば、10進数を2進数に変換することが出来ます。
\(N=B_0+B_1+2(B_2+B_3\times2^1+B_4\times2^2+B_5\times2^3\)・・・\(B_n\times2^{n-2})\)
この計算を簡単にできる方法があります。それがすだれ算です。
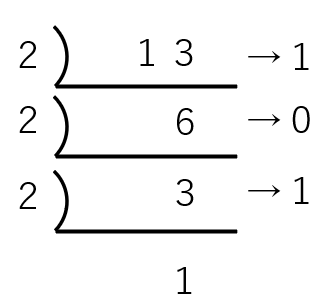
上の計算では、10進数の13を二進数に変換する過程をあらわしています。10進数を2で割った余りを横に、商を下に記述します。商が1になるまで2で割り、余りを下から並べることで2進数に変換出来ます。そのため、13を2進数に変換した結果は「1101」となります。
10進数と小数点以下
小数点以下の2進数を、10進数に変換する場合も、これまでと同様の方法を用います。2進数の0.1は10進数で0.5、2進数の0.01は10進数で0.25…桁が小さくなるごとに、2の乗数だけ小さくなっています。これらを足し合わせることによって10進数に変換することが出来ます。
\(1\times2^{-1}+1\times2^{-2}+1\times2^{-3}\)・・・
小数点以下の10進数を、2進数に変換するとき、10進数をN、2進数の小数第一位をB1、小数第二位をB2…n桁目までとすると
\(N=B_1\times2^{-1}+B_2\times2^{-2}+B_3\times2^{-3}+B_4\times2^{-4}\)・・・\(B_n\times2^{-n}\)
2のB1以降の式を2の-1乗で括ると次のようになります。
\(N=2^{-1}(B_1+B_2\times2^{-1}+B_3\times2^{-2}+B_4\times2^{-3}\)・・・\(B_n\times2^{-n+1})\)
この式から、B1はNを2で掛けた時の整数部分に相当することが分かります。また、小数点以下が2進数の2桁以降になっています。そのため、n桁目になるまでこれを繰り返せば、10進数を2進数に変換することが出来ます。
\(N=2^{-1}(B_1+2^{-1}(B_2+B_3\times2^{-1}+B_4\times2^{-2}\)・・・\(B_n\times2^{-n+2}))\)
同様に、計算を簡単にします。
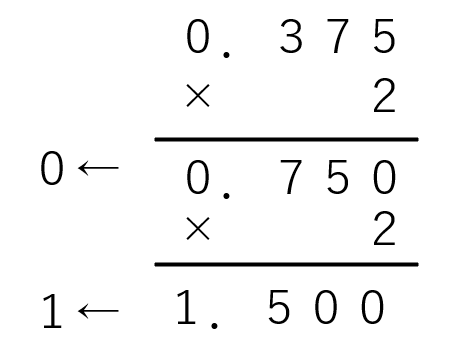
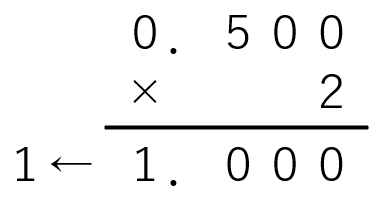
上の計算では、10進数の0.375を二進数に変換する過程をあらわしています。小数点以下の数字に対して、掛け算のひっ算のように2を掛けていきます。小数点以下が0になるまで2を掛け、上から整数部分を並べることで2進数に変換できます。そのため、0.375を2進数に変換した結果は「0.011」となります。
変換する数によっては、無限小数になる場合もあります。
2進数の計算(加算・減算)
加算
10進数と同じように加算することが出来ます。10進数で2+8や、5+5が10になるのと同様に、2進数では1+1が10になります。計算に困った場合は、ひっ算を行うとわかりやすくなります。
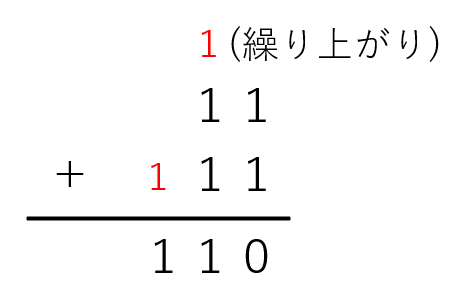
減算
10進数と同じように減算することが出来ます。10進数で10-2が8になるのと同様に、2進数では10-1が1になります。計算に困った場合は、ひっ算をおこなうとわかりやすくなります。

2進数の表記方法(負数・小数)
負の数のあらわし方
符号表記
2進数の最上位桁を符号に割り当ててあらわします。正の数は0、負の数は1になります。
2の補数表記
3桁まで2進数どうしで加算を行います。例えば、101+011は1000です。この場合、3桁までの計算なので、答えは000になります。この時、101から101を引いた時と同じになります。そのため、011は101を負の数で表現していることになります。これを2の補数と呼びます。
\(110+\color{red}{010(2の補数)}\)\(=(1)000\)
2進数の0と1を全て反転したものを1の補数と呼ます。1の補数に1を加えることで、2の補数になります。
\(011\)→\(100\)(1の補数)→\(101\)(2の補数)
小数の表し方
固定小数点数
固定小数点数は、小数点がどの位置にあるかで数値をあらわします。整数では最下位桁の右側が小数点と考えることができます。
例
\(1.001\)
浮動小数点数
浮動小数点数は、指数表記で数値をあらわします。2進数の数値を、mを仮数部、eを指数部として、10進数であらわすと下のようになります。
\(\pm m\times2^e\)
これを2進数であらわす場合、符号、指数部、仮数部の順で並べて表記します。
| 符号1or0 | 指数部e | 仮数部m |
桁の割り当て方には32ビットの形式例、IEEE754の形式例があります。符号は、負の数を1、正の数を0であらわします。
32ビット形式例
符号に1桁、指数部に7桁、仮数部に24桁を合わせて32桁であらわす形式です。負の数の場合は2の補数で指数部を表現します。指数部は絶対値で表示し、0.mの形にしたときのmの部分が入ります。
IEEE754の形式
符号に1桁、指数部に8桁、仮数部に23桁を合わせて32桁であらわす形式です。負の数を含む表現を正の数であらわすために、指数部に予め127を足します。指数部は絶対値で表示し、1.mの形にしたときのmの部分が入ります。
127は、2の8乗を2で割った値から1を引いた数です。指数部は-127が0、127が128になります。
シフト演算(応用)
左シフト
2進数の桁を1つ左にずらすと、10進数の2をかけたものと同じになります。はみ出した数字は削除し、桁を左にずらしてい空いたスペースに0を入れることを、左論理シフトと呼びます。シフト後の数は元の数の2の乗数倍です。
符号をあらわす最上位桁を固定する場合は左算術シフトと言い、負の数も用いることができます。
左シフト演算によって、意味を持つはずの値が削除されてしまう「オーバーフロー」が起こることがあります。これが起こるとシフト演算の結果がおかしくなってしまいます。
例1:左論理シフトのオーバーフロー
\(1101\)ー2桁左論理シフト→\(0100\color{red}{\times}\)
1がはみ出した場合
例2:左算術シフトのオーバーフロー
\(10110\)ー2桁左算術シフト→\(11000\color{red}{\times}\)
符号をあらわす最上位桁と異なる数がはみ出した場合
右シフト
2進数の桁を1つ右にずらすと、10進数の2で割ったものと同じになります。はみ出した数字は削除し、桁を右にずらしてい空いたスペースに0を入れることを、右論理シフトと呼びます。シフト後の数は元の数の1/2の乗数倍です。
空いたスペースに符号をあらわす最上位桁と同じ数を入れた場合を右算術シフトと言い、負の数も用いることができます。
左シフト演算によってはみ出した数は、割り算の結果の余りになります。0がはみ出した時は1/2の乗数で割り切ることが出来ます。



コメント